Parallele Systeme
并行系统(Parallele Systeme)的一些特性(Eigenschaften):
确定性(Determiniertheit):
在相同条件下,产生相同的结果。
无干扰性(Störungsfreiheit):
在遵守既定的并行事件执行顺序的前提下,结果不受影响。
互斥访问资源(Wechselseitiger Ausschluss exklusiv nutzbarerer Ressourcen,mutual exclusion):
每一时刻最多只有一个进程可以访问共享资源(该资源被独占使用)。
无死锁(Verklemmungsfreiheit,Deadlock free):
没有多个进程间的循环等待情况。
无饥饿(Kein Verhungern,Starvation free):
不会有进程因为被一直推迟执行而永远得不到资源。
我们这里主要关注一个用于形式建模的方法:Petri-Netze。
Petri-Netze
Petri-Netze主要是关注状态以及状态变化(Zuständen und Zustandsüberg.ngen)。
首先先来看定义:
一个 Petri 网是一个三元组 (S, T, F),其中:
S:有限集合,称为“Stellen”(位置 / 状态)用圆圈表示。
表示被动元素,例如:存储单元、资源。
T:有限集合,称为“Transitionen”(变迁 / 转换)- 用矩形表示。
- 表示主动元素,例如:处理器、事件、过程。
F:流关系(Flussrelation)- $F \subseteq (S \times T) \cup (T \times S)$
- 用有向边(gerichtete Kanten)表示。
- 并且满足:$S \cap T = \emptyset$ 。
每个Knote $x \in (S \cup T)$的
- Vorbedingung 指的是:$\bullet x := \{ \ y \ | \ y \ F \ x\ \}$,即能到x的点
- Nachbedingung 指的是:$ x \bullet := \{ \ y \ | \ x \ F \ y\ \}$,即x能到的点。
例子:
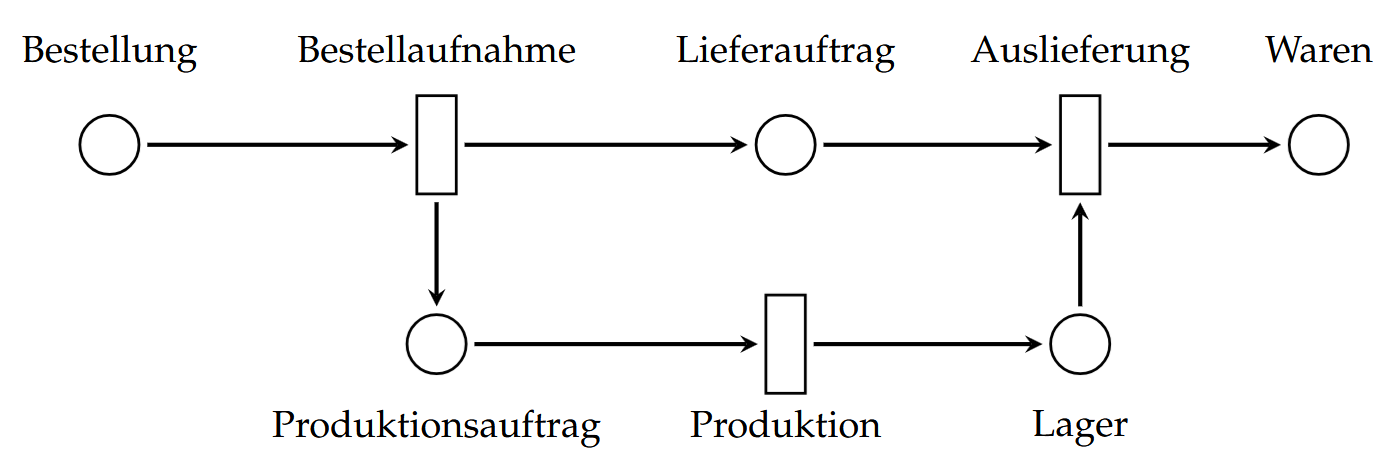
和其他的建图一样,我们这里也可以定义带有标记(即容量,权重等)的图:
Kapazität einer Stelle:$c : S \to \mathbb{N}_0 \cup \{\infty\}$
如果没有专门标记出来,则默认 $\infty$。
Gewichtung einer Kante:$w : F \to \mathbb{N}_0$
如果没有专门标记出来,则默认 $1$。
一个位置-变迁网(Stellen-Transitionsnetz)里除了上面提到的2个函数还需要一个函数
$M : S \to \mathbb{N}_0 \cup \{\infty\}$
用于描述图当前的状态(Aktuelle Belegung des Netzes),即每个Stelle里的Token数量。
需要满足 $\forall s \in S: M(s) \leq c(s)$。
一个位置-变迁网(Stellen-Transitionsnetz)叫做Bedingungs/Ereignisnetz 或 Boolesches Netz(布尔网络),当$M : S \to \mathbb{B}$ ,也就是说每个Stelle里最多可以有1个Token。
触发规则(Schaltregel)
一开始我们就提到,我们的关注点主要是系统的状态以及状态的变化。在前面介绍的内容中,函数 $M$ 被用来描述系统的当前状态,而我们希望通过 $T$(即Transitionen的集合)来描述状态的变化过程。不过,任何状态的变化都必须满足一定的前提条件。那么接下来我们就来看看,在 Petri 网中,这些条件是如何被定义的。
给定一个位置-变迁网(Stellen-Transitionsnetz),即一个Petri-Netz (S, T, F),函数 $c, w, M$。
一个Transition $t \in T$ 可以触发(kann schalten)当:
- $\forall s \in \bullet t: M(s) \geq w(s, t) $
- $\forall s \in t\bullet: M(s) \leq c(s) - w(t, s)$
即当:
- 到 t 的Stelle里有足够的Token(至少 $w(s, t)$ 个)
- t 能到的所有Stelle里有足够的空位给 $w(t, s)$ 个Token
时才能触发 t 。
这个t触发后整个图的状态会变成$M’$:
- $\forall s \in \bullet t \setminus t\bullet: M’(s) = M(s) - w(s, t)$
- $\forall s’ \in t\bullet \setminus \bullet t: M’(s’) = M(s’) + w(t, s’)$
- $\forall s’’ \in \bullet t \cap t\bullet: M’(s’’) = M(s’’) - w(s’’, t) + w(t, s’’)$
例子:
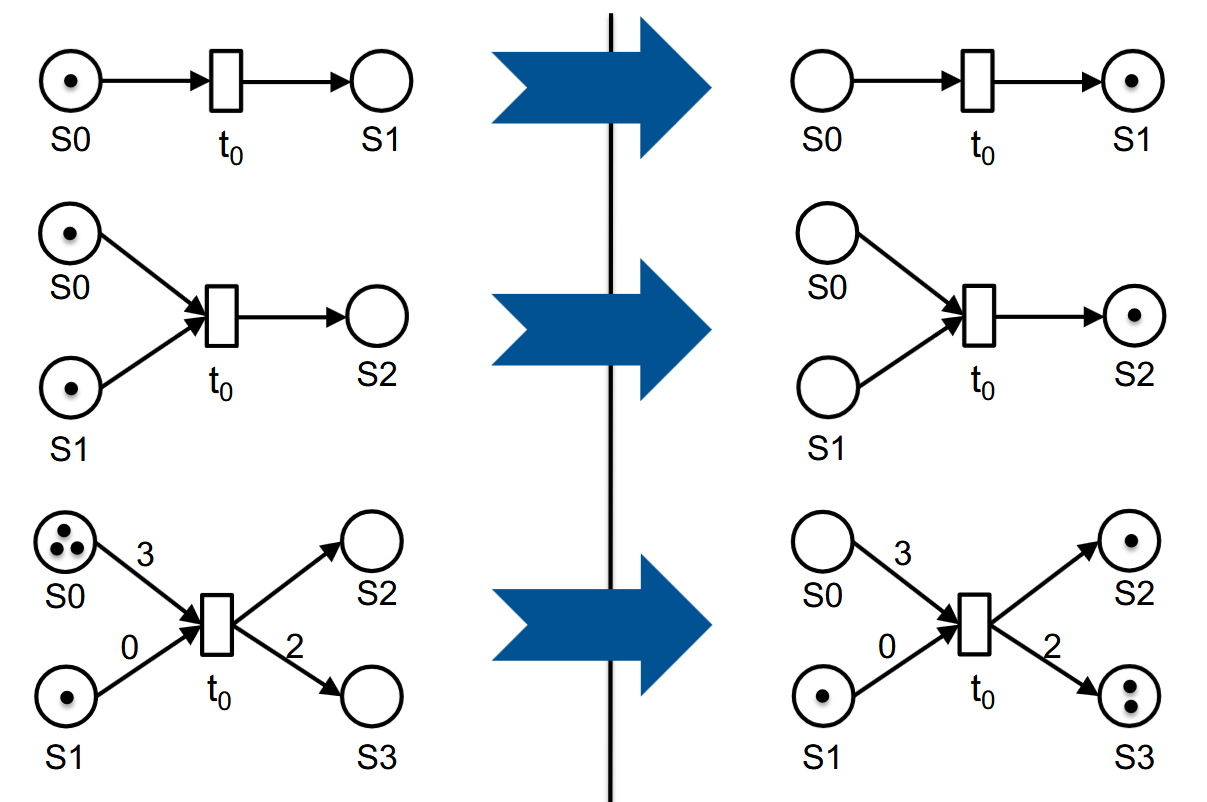
因为没有专门标记出来,所以默认Kapazität是 $\infty$,Gewicht是1。
不能Schalten的例子:
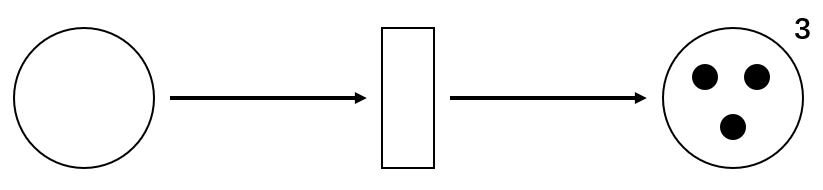
因为后面那里已经没有空余的位置了。
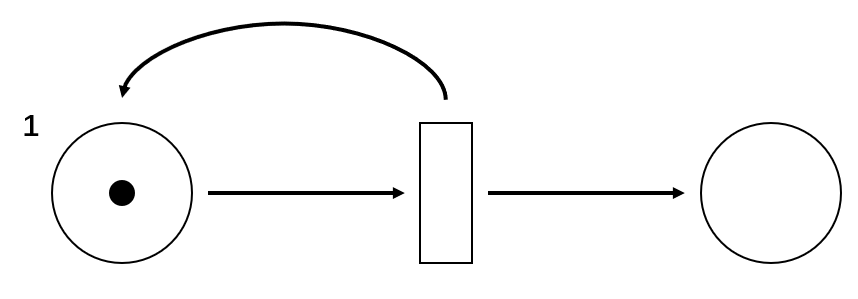
这个同样不行,因为这里Schalten需要考虑3个地方:
- 左边的s是否有足够的(1个)Token来触发t
- 左边的s是否有足够的空闲位置
- 右边的s是否有足够的空闲位置
很明显第二点并不满足。
注意,这里不能想着说反正左边的token会在触发 t 的时候被消耗掉所以就有足够的空闲位置!!!
一定要所有的前提条件都满足了才能触发 t 。
接下来我们来看一下怎么样可以通过建模出来的图判断当前系统的一些属性:
并发性 / 并行性(Nebenläufigkeit,Concurrency)
两个Transitionnen $t_0$ 和 $t_1$ 是并发的(nebenläufig),当它们可以互不干扰地独立触发(unabhängig von einander schalten können, ohne sich gegenseitig zu beeinflussen.)。
例子:
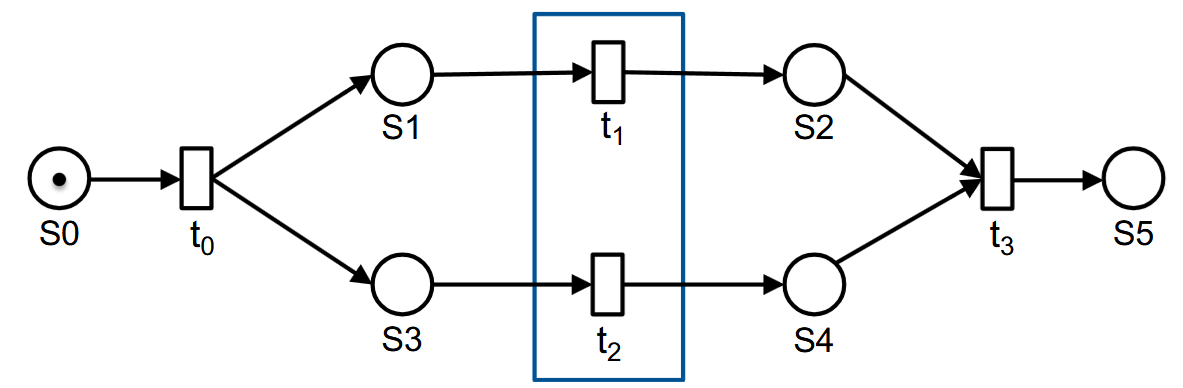
可以看到,这里的 $t_1$ 和 $t_2$ 是并发的(nebenläufig),但 $t_1, t_2$ 和 $t_3$ 明显不是,因为 $t_3$ 只有在 $t_1, t_2$ 被触发后才能被触发。
不确定性(Nichtdeterminismus)
不确定性表示在给定的标记状态 $M$ 下,可能会出现关于Transitionen可触发性的冲突。
而 $t_0$ 和 $t_1$ 处于冲突中(stehen im Konflikt),当它们共享输入或输出的位置,并且这些位置的 token 数量只能满足其中一个Transition的触发条件。
如果token的数量足够触发所有的Transitionen那就不算有冲突,整个图也是确定的(deterministisch)。
这样会导致进行一次不确定的选择(nichtdeterministische Auswahl)。
例子:
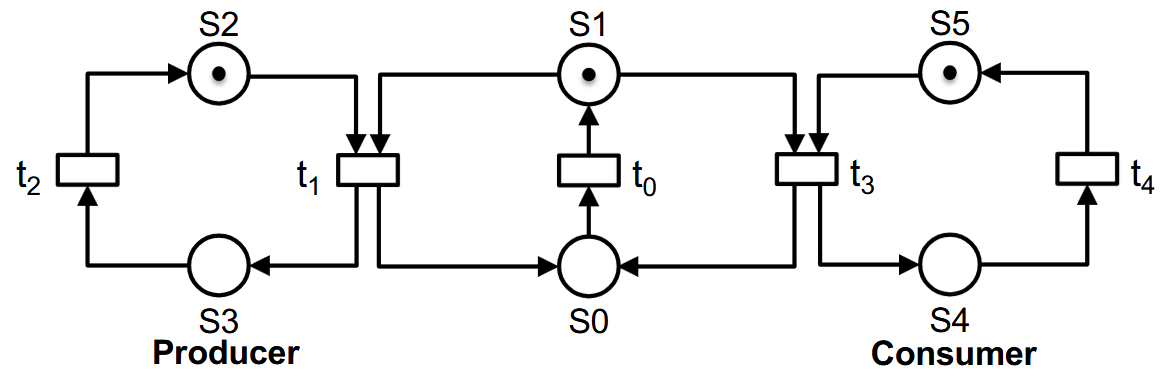
这里的 $t_1$ 和 $t_3$ 冲突了,因为s1里只有1个token,所以要么触发 $t_1$ ,要么触发 $t_3$。
可到达性(Erreichbarkeit)
给定一个一个Petri-Netz (S, T, F) ,c,w,以及一个初始状态 $M_0$ 。
那么一个有限序列(endliche Sequenz)$\rho = t_0, t_1,…, t_n \ (\text{with } t_i \in T)$ 被叫做由 $M_0$ 激活的有限切换序列(von M aktivierteendliche Schaltfolge),当存在 $M_1, M_2,… M_n$ 使得:
如果存在一个有限序列使得 $M$ 能变成 $M’$ ,那么我们就说 $M’$ ist von $M$ erreichbar。
针对这个Erreichbarkeit我们可以再建立个图,叫做 Erreichbarkeitsgraph。里面的点表示 Belegung,有向边表示 Transition。
例子:
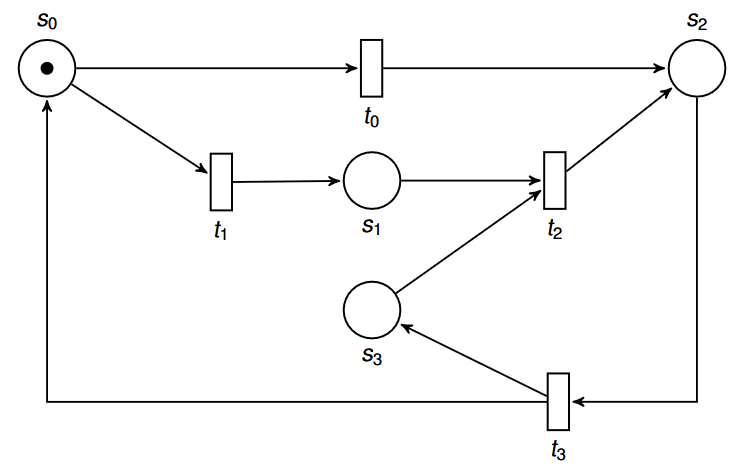
它对应的Erreichbarkeitsgraph:
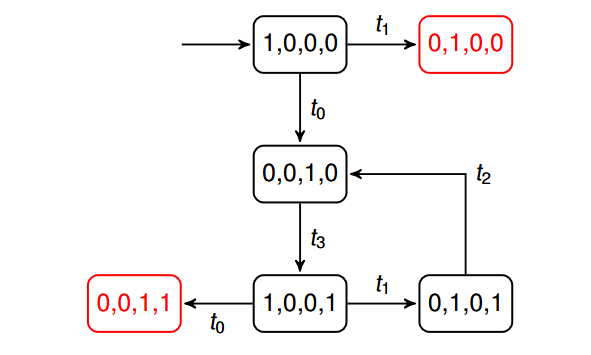
记得左上角的这个有向边一定要画!
注意:每个Petri-Netz会有着唯一的一个Erreichbarkeitsgraph,但一个Erreichbarkeitsgraph可能会对应很多个Petri-Netz,因为可能存在一些永远无法触发的Transitionen(这些无法触发的Transitionen完全不会改变Erreichbarkeitsgraph)。
Lebendigkeit(liveness)
给定一个一个Petri-Netz (S, T, F) ,c,w,以及一个初始状态 $M_0$ 。
它是活跃的(lebendig),当对于所有 $t \in T$ 都满足以下条件:
对于所有从 $M_0$ 可到达的状态 $M_1$,存在一个后续状态 $M_2$, 使得 $t$ 在 $M_2$ 中可以触发,且 $M_2$ 是从 $M_1$ 可达的,即
死锁(Verklemmung, Deadlock)
给定一个一个Petri-Netz (S, T, F) ,c,w,以及一个初始状态 $M_0$ 。
从 $M_0$ 出发可达的某个标记 $M$,称为完全死锁状态(vollständige Verklemmung),如果在该状态下没有任何Transition $t \in T$ 可以触发。
如果一个Netz是lebendig的,那么它一定是verklemmungsfrei。(lebendig $\Rightarrow$ verklemmungsfrei)
但一个Netz是verklemmungsfrei不一定能够说明它也是lebendig的。(verklemmungsfrei $\nRightarrow$ lebendig )
Verhungern(Starvation),Fariness
给定一个一个Petri-Netz (S, T, F) ,c,w,以及一个初始状态 $M_0$ 。
Eine Transaktion t ∈ T verhungert, 当存在一个无线序列使得t尽管处于可触发的状态但是只被触发了有限次。(wenn es eine unendliche Sequenz gibt, in der t trotz Transitionsbereitschaft nur endlich oft auftritt.)
注意这里的前提条件“处于可触发的状态”非常重要,这个如果不满足那么就不能叫verhungert。
一个Netz是公平的(fair)的,当不存在某个无限序列(例如 $t_0 \to t_4 \to t_1 \to \dots$),使得变迁 $t$ 虽然始终处于可触发状态,却永远没有或只有有限次被实际触发。
所以如果一个Netz是公平的,那么就没有Transition会挨饿(verhungert)。
例子:
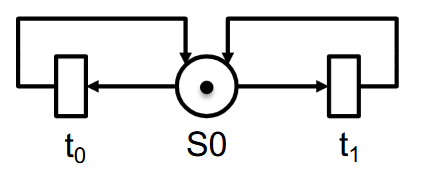
这个Netz是不公平的(unfair),因为存在
- $t_0 \to t_0 \to t_0 \to \dots$ ,即 $t_1$ 会挨饿;
- $t_1 \to t_1 \to t_1 \to \dots$ ,即 $t_0$ 会挨饿;
例子:
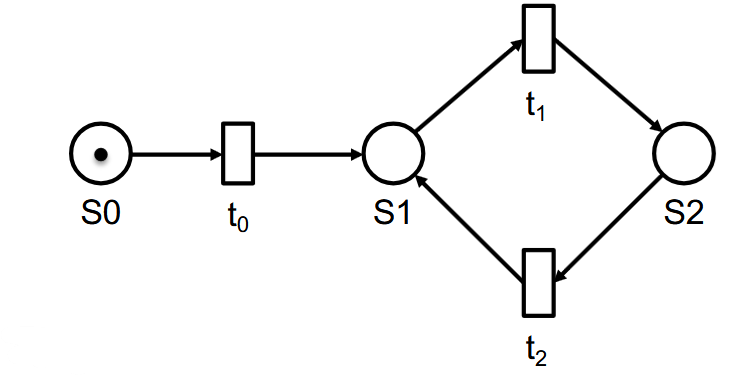
这个图是:
nicht lebendig
因为t0只能被触发一次。
deadlockfrei
进到右边那个圈里之后永远都可以有后续操作。
fair
因为t0触发一次之后不可能再进入准备就绪的状态,所以不算挨饿。




